The Wire
The basic material is wire rod, which is cold-drawn to differnt dimensions and strenght grades. The most common grades are:
| Rope grade | Wire tensile strength grades | Hardness app. | |||
|---|---|---|---|---|---|
| EN | API 9A | Min | Max | Brinel | Rockwell |
| N/mm² | N/mm² | HB | HRC | ||
| 1570 | PS | 1370 | 1770 | 405/425 | 45 |
| 1770 | IPS | 1570 | 1960 | 445/470 | 49 |
| 1960 | EIPS | 1770 | 2160 | 470/480 | 51 |
| 2160 | EEIPS | 1960 | 2160 | 480/500 | 52 |
Finish
The wire is either untreated (bright), galvanized or stainless. Galvanized wire gives the rope higher protection for especially corrosive environment. For extream cases a stainless rope is used. Steel wire ropes can also be provided with plastic impregnation.
Properties of Extension of Steel Wire Ropes
Any assembly of wires spun into a helical formation (either as a strand or a wire rope), when subjected to a tensile load, can extend in three seperate phases, depending on the magnitude of the applied load:
Phase 1: initial extension
Phase 2: elastic extension
Phase 3: permanent extension (thermal elongation and contraction, rotation, wear and corrosion)
Phase 1 and 2 are highly important because they represent a part of the qualities of the rope. Phase 3, on the other hand, can be caused by wrong choose of rope or lack of rope inspection. The phases are connected to eachother and cause a course of event in all ropes that are exposed to gradual increased load. Due to this a new rope, which are exposed to overloading, will go through phase 1 and 2 before the third phase (permanent extension) begin.
Phase 1: Initial or permanent extension
This phase of extension of the rope depend on the construction of the rope and can be explained as following:
When loading a new product, extension is created by the bedding down of the assembled wires with a corresponding reduction in overall diameter. This reduction in diameter creates an excess length of wire which is accommodated by a lengthening of the helical lay.
When sufficientely large bearing areas have been generated on adjacent wires, to withstand the circumferential compressive loads, this mechanically created extension ceases and the extension in phase 2 commences.
The initial extention can not be accurately determined and depend on, apart from the strand or the rope construction, the various load and the current load frequency.
It is not possible to quote any exact values for various constructions but the following approximate values can be used to give reasonably accurate results.
| Load | Safety factor | Extension in % of the total length of the rope | |
|---|---|---|---|
| Rope with fibre core | Rope with steel core | ||
| Lightly loaded | 8 | 0,25 % | 0,125 % |
| Normally loaded | 5 | 0,5 % | 0,25 % |
| Heavily loaded | 3 | 0,75 % | 0,5 % |
| Heavily loaded with many "bends" | 2 | 2 % | 1 % |
Phase 2: Elastic extension (elongation)
Following Phase 1, the rope extends in a manner which complies approximately with Hookes Law, i.e. stress is proportional to strain.
The proportionality factor normally is a material constant called Modulus of Elasticity (E-module). To steel wire ropes the E-module is more of a construction constant than a material constant.
The elastic extension can be calculated as followed (Hookes law):
Elastic extension (mm) = (W x L) / (E x A)
W = applied load (kg)
L = rope length (mm)
E = elastic modulus (kg/mm2)
A = area of rope - circumscribed circle (mm2)
The modulus of elasticity varies with different rope constructions. According to manufacturing factors, wire dimensions and a lot of other factors the E-module various between different wire ropes of the same construction and dimension. If exact E-module olf a certain rope is necassary a modulus test have to be done at that rope.
The elastic extension is valid until the proportionality or elasticity limit is reached. By load exceeding this limit extension according to phase 3 take place. Elasticity limit are defined as the largest strain where the rope return to its original length when unloaded.
General E-module of the rope construction
| Type of steel wire rope | E-module |
|---|---|
| kp/mm² | |
| 1x7 | 12600 |
| Compacted 1x7 | 14000 |
| 1x19 | 10900 |
| Compacted 1x19 | 13600 |
| 6x7+FC | 6300 |
| 6x7+WRS | 7000 |
| 6x36+FC | 5000 |
| 6x36+IWRC | 6000 |
| Compacted 6x36+IWRC | 6400 |
| Compacted DSC8 | 7900 |
| 18x7 | 4200 |
| 35x7 | 6900 |
| Compacted 34x7+WSC | 7200 |
| 18x19S+FC | 4000 |
| 18x19S+IWRC | 6000 |
| These values are current for ropes operating with safetyfactor 5:1. By lower safety factors the module of elasticity indicated are raised and by higher safety factors they sink. | |
Phase 3: Permanent extension
Load that cause tension in the steel wire rope, which exceeding the yield point of the material, the linear relation, due to phase 2, between stress and strain. This mean a small increase of load cause a lager extension than it would be in the elastic elongation area. If the load continues to increase the extension will increase faster than the load. This relation accelerate until a condition of permanent extension is reached and finally of the rope without further loading.
Thermal expansion and contraction
This type of extension or contraction depend on the coefficient of linear expansion of the rope.
The coefficient is linear depending on the teperature variation of the material and has the value: 0,0000125/˚C.
The formula for length extension is following: Extension in m = 0,0000125 x L x t.
L = length of rope (m)
t = temperature change (˚C)
Extension due to rotation
The elongation can be caused by a free rope end being allowed to rotate when loaded, e. g. "free" load or montage of swivel. The lay will be extended and cause an elongation.
Extension due to wear
The elongation due to inter-wire wear reduces the cross-sectional area of steel and producesextra constructional extension.
Exampel:
The total elongation of a 200 m length of steel wire rope type 28 mm 265-wires (6x36-IWRC) at a tension of 10 tons (safety factor 5:1) and with an increase in temperature of 20°C.
According to phase 1:
Permanent constructional extension = 0,25% x total rope length = 0,25% x 200 m = 500 mm.
According to phase 2:
Elastic extension = (W x L) / (E x A) = (10000 x 200000) / (6000 x 615,8) = 540 mm.
According to phase 3:
Thermal expansion = 0,0000125 x L x t = 0,0000125 x 200 x 20 = 50 mm.
Total extension = 500 mm + 540 mm + 5+ mm = 1090 mm.
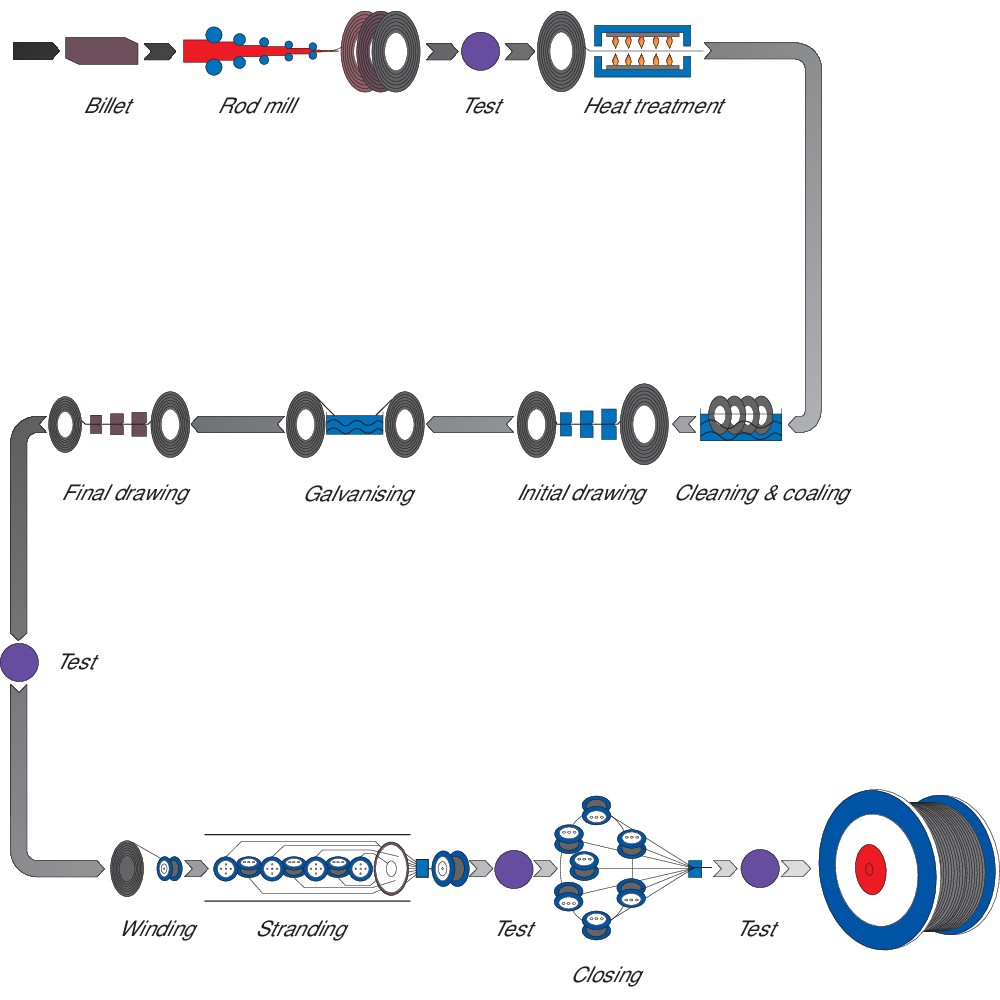
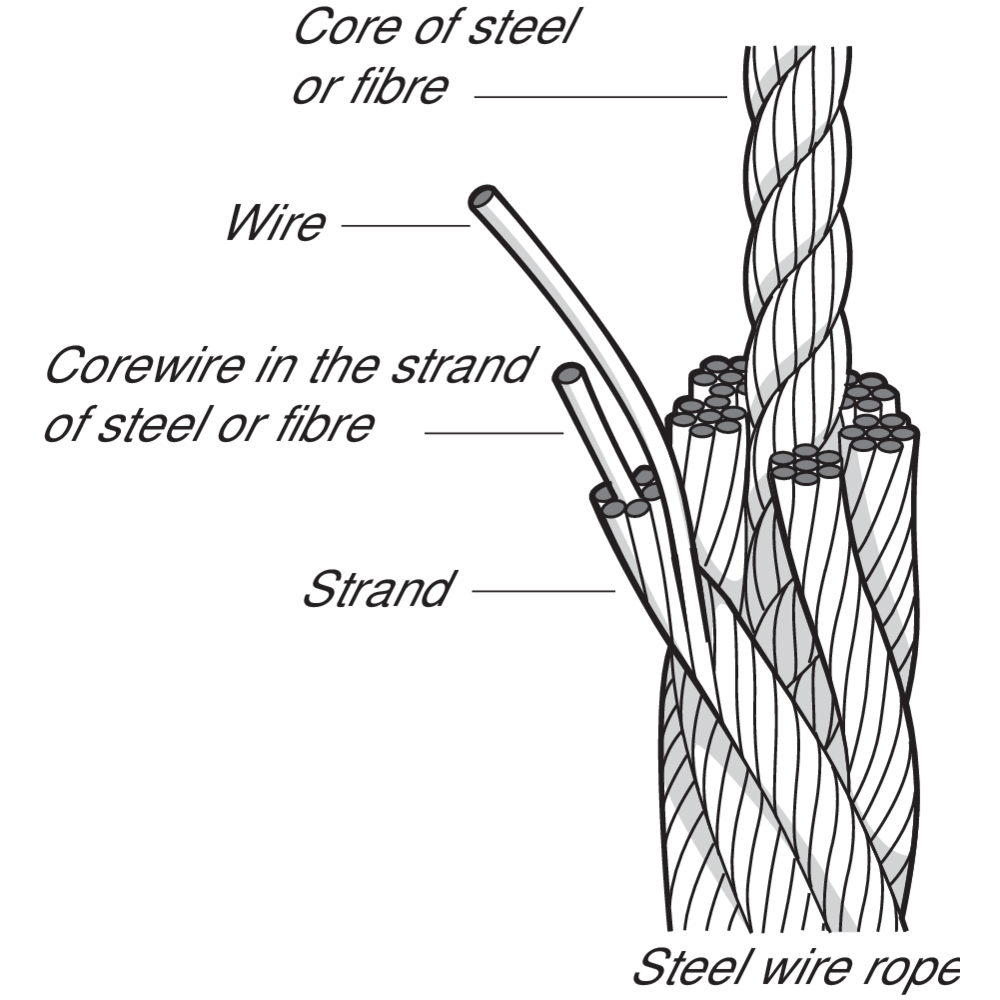
From Rod to Rope



To Choose Steel Wire Rope
When ordering steel wire rope, ensure about right type, construction, dimension and length. Follow the machine manufacturers recommendations and assure that the equipment has the right machine group/grade.
WARNING! Wrong choice of steel wire rope can cause reduced working life, fracture of rope and/or damage of equipment.
The following questions can help you to choose the right construction of ropes. If you have conflicting answers, you shall choose the most frequent alternative. Putting together the ten answers will help to choose the most optimum rope construction, but other questions and/or considerations can sometimes lead to another rope construction. For further advice, please contact CERTEX.
| 1 | Rotation resistance" demanded? | "Rotation resistent" rope | "Rotation resistent" rope | 6/8/9/10-strand rope |
|---|---|---|---|---|
| 1 | "Rotation resistance" demanded | "Rotation resistent" rope | "Rotation resistent" rope | 6/8/9/10-strand rope |
| 2 | High braking load demanded? | Special rope, compacted | Rope with steel core | - |
| 3 | Lots of bending? | Multistrand rope with small outer wires | Multistrand rope with small outer wires | - |
| 4 | Large outer wear? | Rope with large outer wires | Rope with large outer wires | - |
| 5 | Coiled in many layers? | Coiled in many layers? | - | Ordinary hand lay rope |
| 6 | Risk of deformation- damage? | Rope with plastic encapsulated core | Rope with plastic encapsulated core | - |
| 7 | Large rope guide angels? | Large rope guide angels? | Rope with plastic encapsulated core | - |
| 8 | Left groove drum | Right hand lay | - | Left hand lay |
| 9 | Left drawn rope guide? | Right hand lay | - | Left hand lay |
| 10 | Corrosive environment? | Galvanized/stainless rope | Galvanized/stainless rope | Bright/galvanized rope |



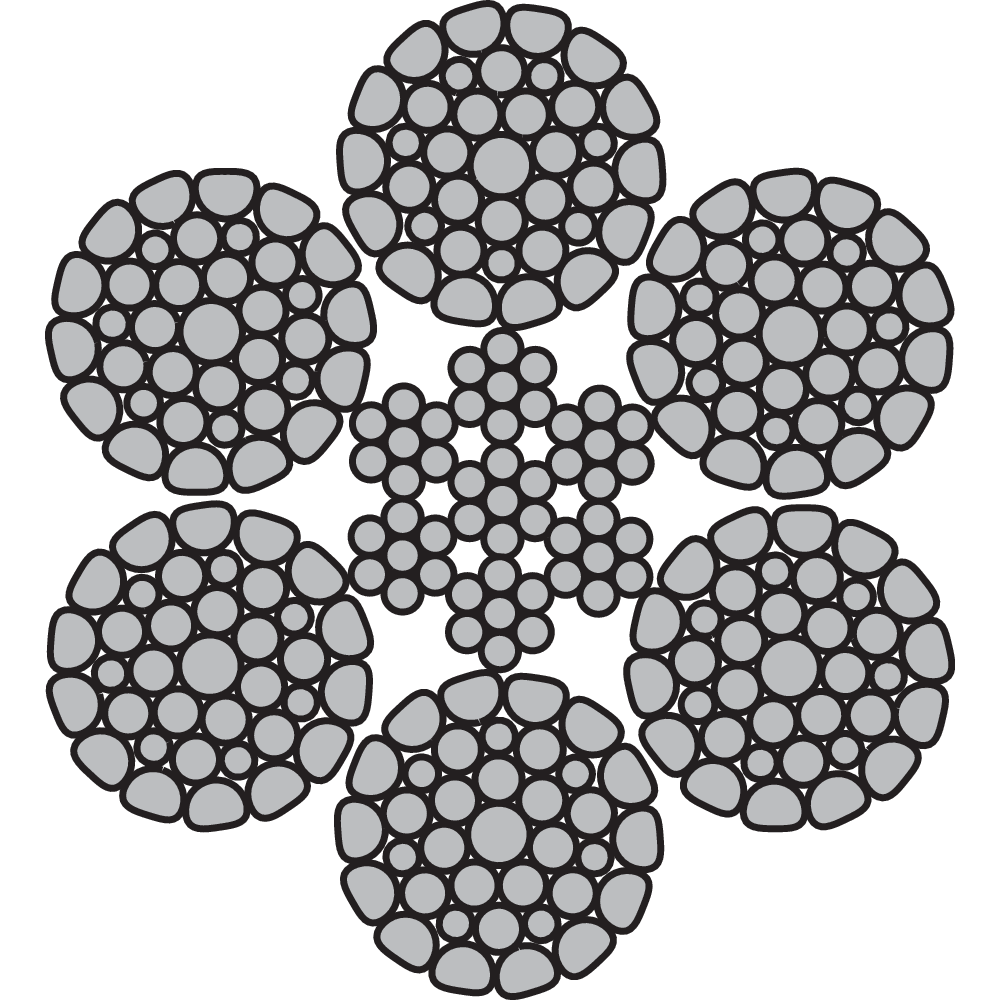
What is a Steel Wire Rope?
A steel wire rope is made up of individual steel wires spun into a strand. A number of strands are closed over a central core thus producing a rope. The number and size of wires must offer the best compromise possible between large wires for maximum corrosion protection and resistance to abrasion, and smaller wires for the necessary flexibility and handling.
The construction of a steel wire rope is expressed according to following:
e.g 6x36-FC
6 is the number of strands in the steel wire rope
36 is the number of wires in the strand
FC is the type of the core



Strand Lay
In a strand construction with several layers of wire of the same diameter the different layers cross each other (cross lay). In an strand construction with unequal wire diameters the layers of wires lie parallel to each other (equal or parellel lay).
In equal laid strands the steel area increases compared to cross lay strands. Other advantages of parallel laid strands are the improved fatigue and wear resistance resulting from the same wire lay length and strand angle.






The Core
The strands in a rope are laid around a core of either fibre, steel or solid plastic.
Where the strands are laid over a fibre core FC is used, e.g. 6x19-FC.
Ropes with steel cores should be chosen if the rope is exposed to high working temperature, hard strains, high work rate, hard pressures on drums and blocks etc. The steel core gives better support for the strands, which result in the rope retaining its shape better and giving a better distribution of the stresses in the individual wires.
If the steel core of the rope consists of a single strand the term -WSC is used, e.g. 6x19-WSC.
If the steel core of the rope consists of a steel wire rope the term -IWRC is used, e.g. 6x19-IWRC.
Some steel wire ropes can have a plastic encapsulated core which provides increased stability to the rope and also reduces the wear and corrosion in and around the core, e.g. Dyform 8 PI.












Rope Lay
Ordinary hand lay
The direction of the lay of the outer layer of wires in the strands is opposite to the direction of lay of the strands in the rope. Ordinary lay is more resistant to kinking and untwisting, and less likely to fail as a result of crushing and distortion.
Lang's lay
The direction of lay of the outer layer of wires in the strands are in the same direction of lay of the strands in the rope. The advantage of using Lang's lay is that the rope offers a better wearing surface when in use, and therefore can be expected, in many cases to last longer. Lang's lay ropes produce relatively high torque values under working conditions and must not be used on applications where one end of the rope is free to rotate or where problems from rope turn are likely to occur.
Right hand lay
The strands are twisted to the right around the core. Right hand lay is the most common lay direction in a rope.
Left hand lay
The strands are twisted to the left around the core.












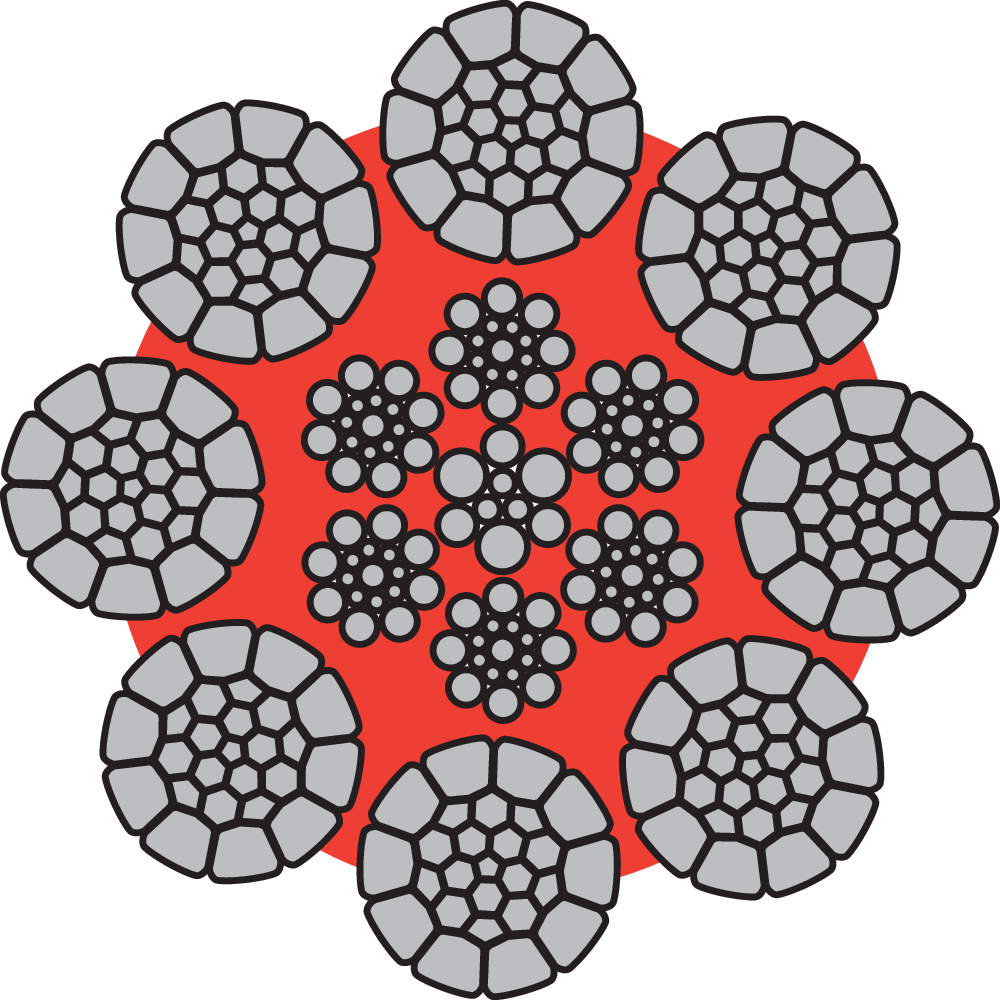
Rotation Resistance
To achive as little rotation tendency as possible with high lifting heights "rotation resistent" ropes should be used.
Rotation resistant ropes are made out of many layers of strands. Every layer are laid in opposite direction to the next layer, so that the torque in the different layers outmatch each other.



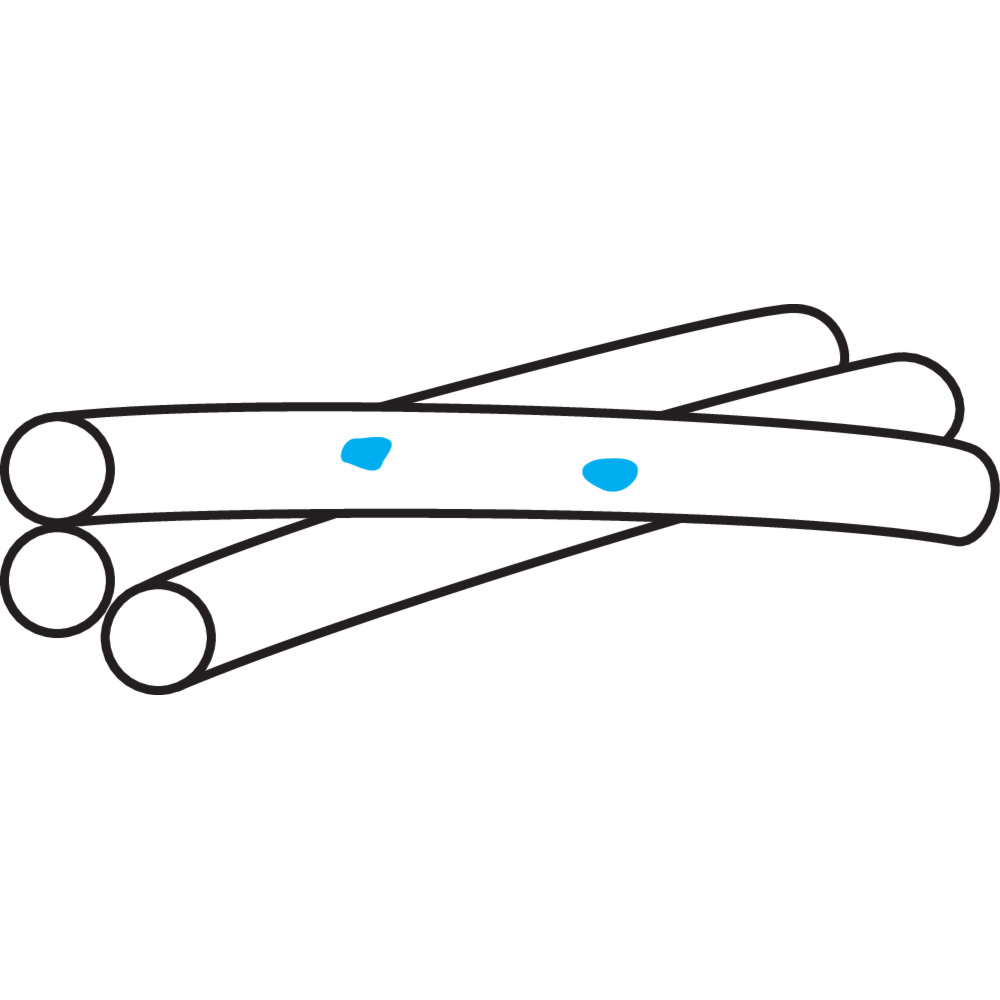
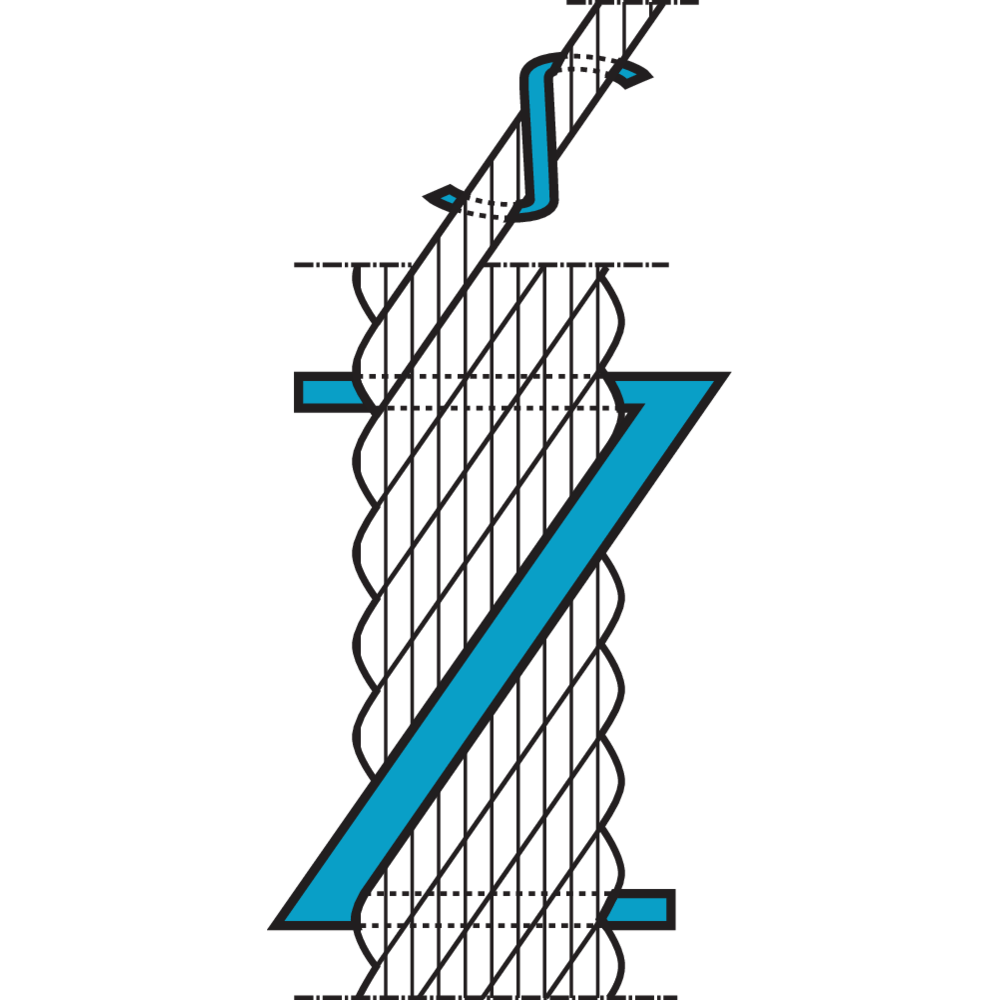
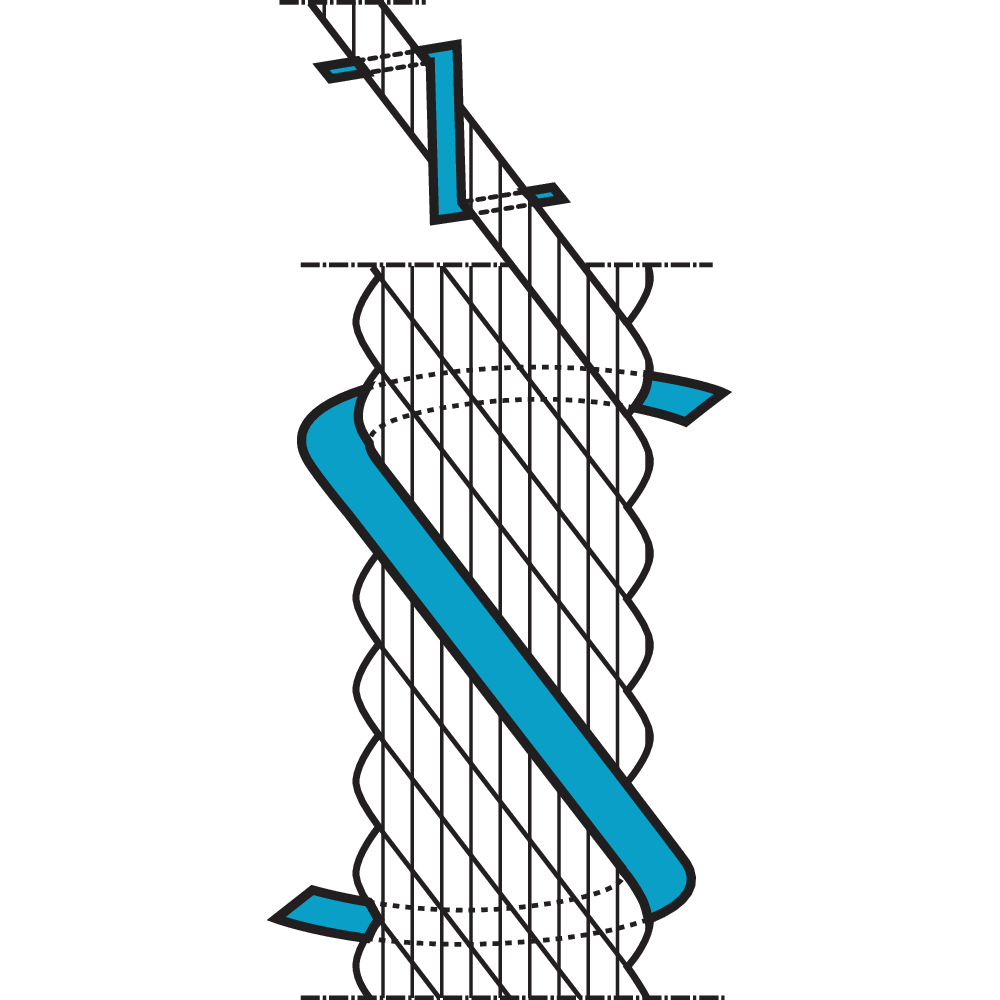
Preforming
Preforming is a type of process assuring that each strand of the rope is preformed to the helical shape it will assume in the finished rope. Advantages of preforming:
– The ropes are free from liveliness and twisting tendencies which makes installation and handling easier.
– The ropes can be cut without seizings and exposed ends will not untwist.
Preforming takes place in a preformhead where the strand pass immediately berfore the closing. Preformed wire ropes has a lot of names, e.g. preformed, trulay.
![Preform[new]_225mm_2](/sites/certex-fi/techdoc_import/Technical%20information%20general/STEEL%20WIRE%20ROPE%20PRODUCTS/OLD_Technical%20information/Steel%20wire%20rope/Technical%20description/10431/image-thumb__10431__general-base/preform-new-_225mm_2.b81e7256.png)
![Preform[new]_225mm_2](/sites/certex-fi/techdoc_import/Technical%20information%20general/STEEL%20WIRE%20ROPE%20PRODUCTS/OLD_Technical%20information/Steel%20wire%20rope/Technical%20description/10431/image-thumb__10431__general-thumb/preform-new-_225mm_2.eeb2ffe7.png)
![Preform[new]_225mm_2](/sites/certex-fi/techdoc_import/Technical%20information%20general/STEEL%20WIRE%20ROPE%20PRODUCTS/OLD_Technical%20information/Steel%20wire%20rope/Technical%20description/10431/image-thumb__10431__general-base/preform-new-_225mm_2.b81e7256.png)
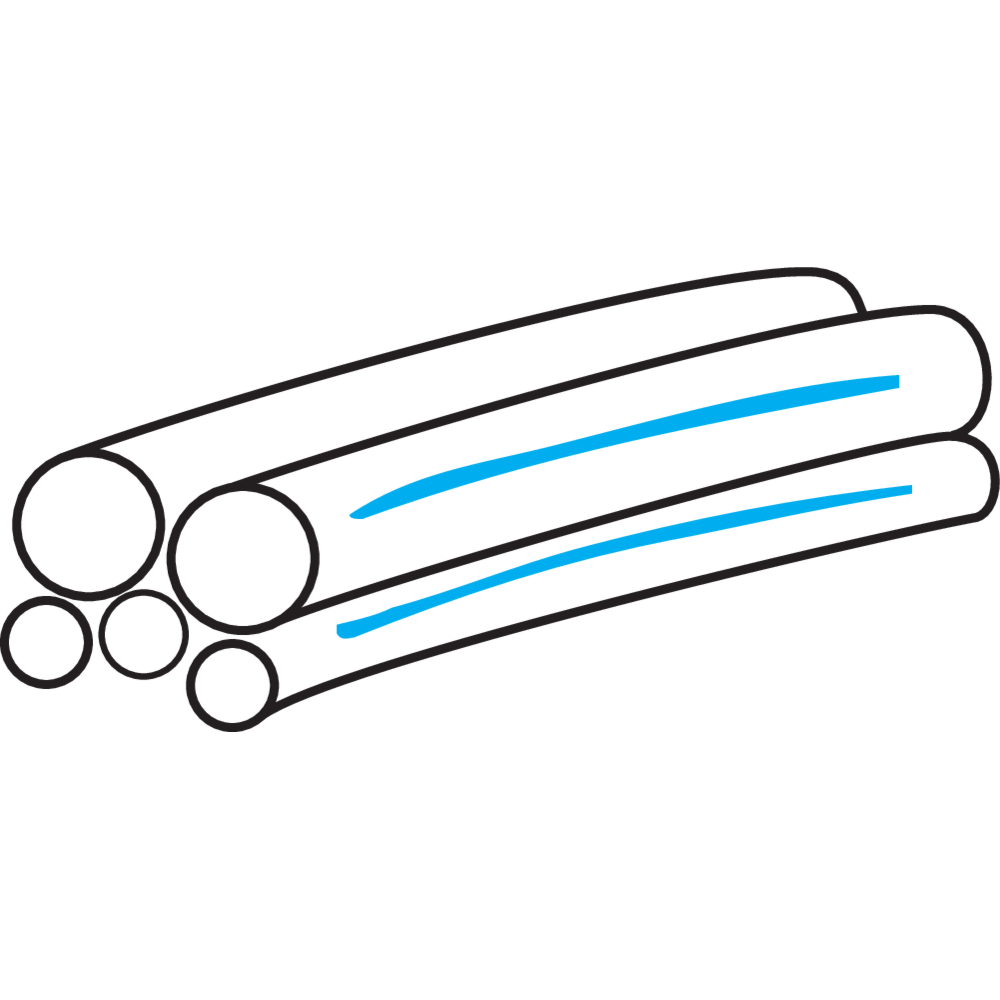
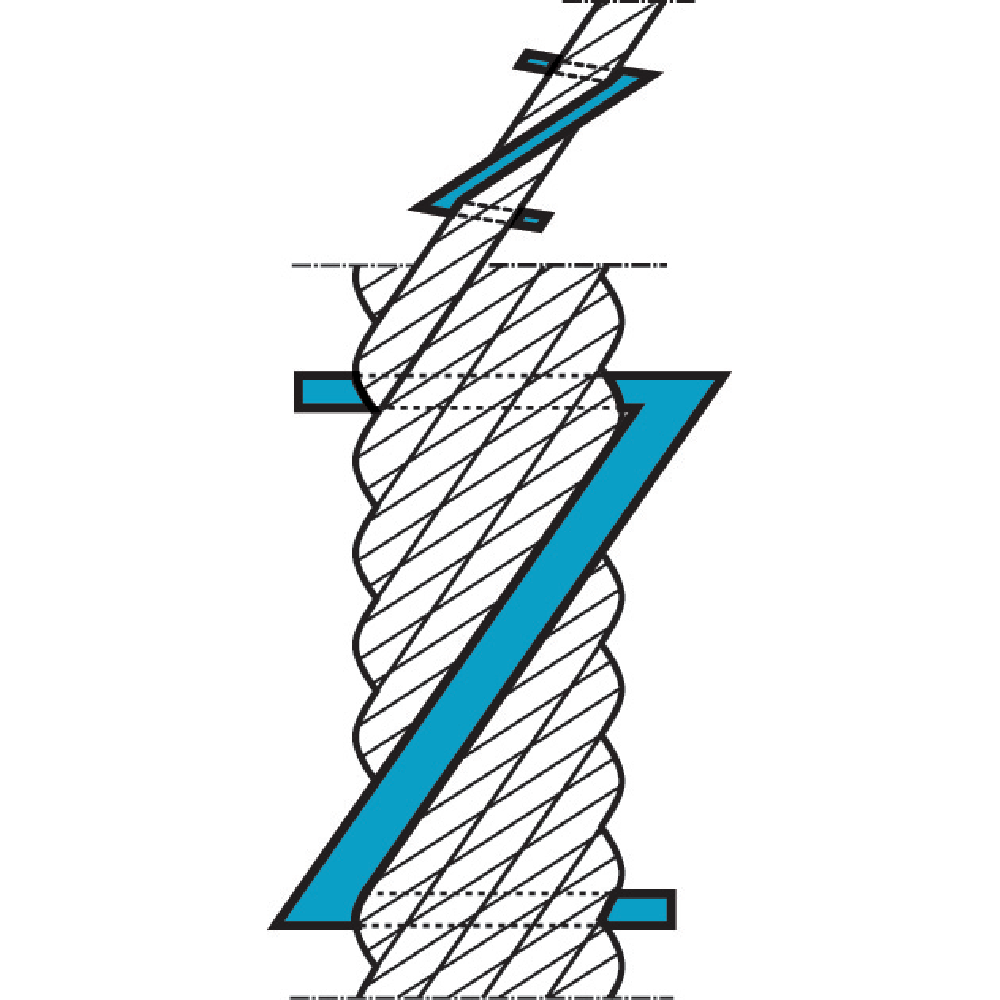
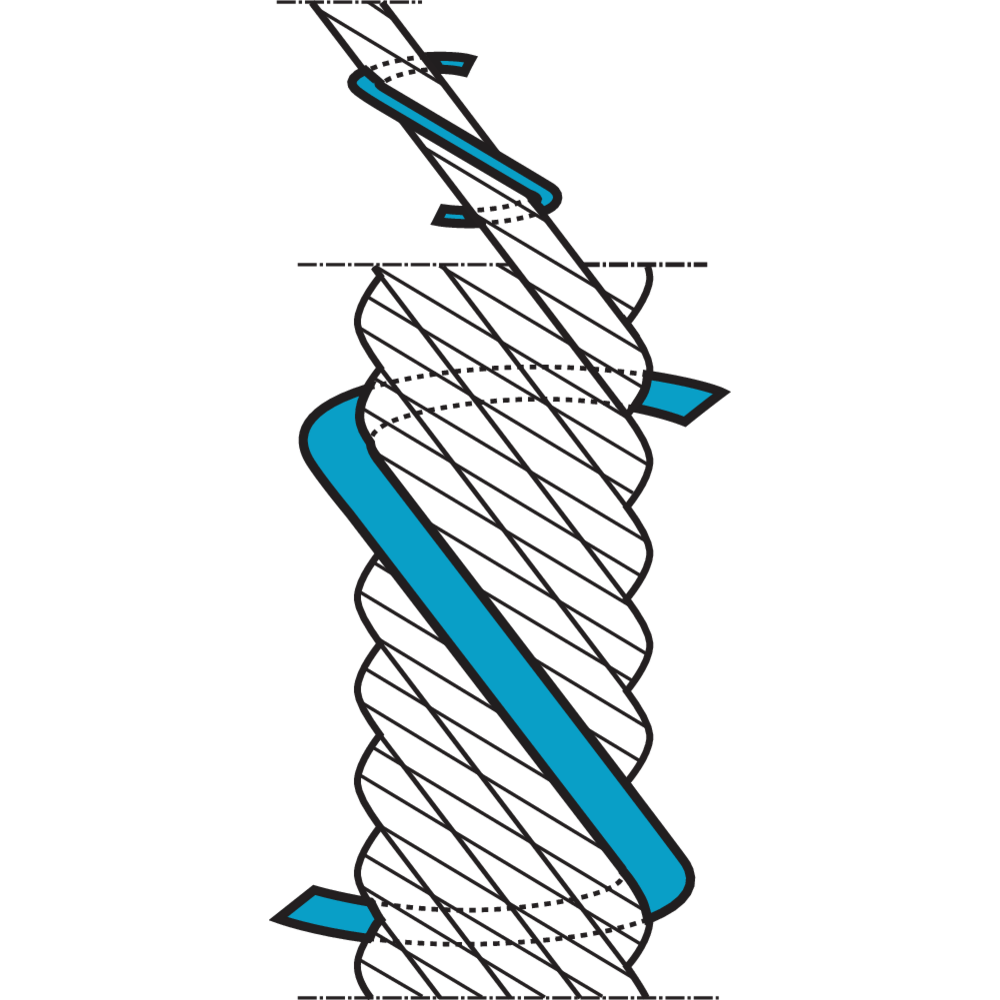
Lay Length
Lay length is an expression for the length on a "wire- or strandhelix". Lay length is carefully decided for each wire rope construction and has to be retained, otherwise the life length of the wire rope is considerably reduced.
![Strand lay length_eng[new]_225mm_2](/sites/certex-fi/techdoc_import/Technical%20information%20general/STEEL%20WIRE%20ROPE%20PRODUCTS/OLD_Technical%20information/Steel%20wire%20rope/Technical%20description/10432/image-thumb__10432__general-base/strand-lay-length_eng-new-_225mm_2.6207213b.png)
![Strand lay length_eng[new]_225mm_2](/sites/certex-fi/techdoc_import/Technical%20information%20general/STEEL%20WIRE%20ROPE%20PRODUCTS/OLD_Technical%20information/Steel%20wire%20rope/Technical%20description/10432/image-thumb__10432__general-thumb/strand-lay-length_eng-new-_225mm_2.0e8a7460.png)
![Strand lay length_eng[new]_225mm_2](/sites/certex-fi/techdoc_import/Technical%20information%20general/STEEL%20WIRE%20ROPE%20PRODUCTS/OLD_Technical%20information/Steel%20wire%20rope/Technical%20description/10432/image-thumb__10432__general-base/strand-lay-length_eng-new-_225mm_2.6207213b.png)
Definitions of Breaking Load
”Minimum breaking load”
Minimum breaking force (minimum breaking load), in kilonewtons/kilopond, below which the rope shall not break when tested to destruction.
Calculated breaking load
The value calculated from the product of the sum of the crossectional metallic areas of all the individual wires in the rope and the tensile strength grade(s) of the wires. The total metallic area is directly proportional to the square of the nominal diameter of the rope. The lay loss that results from the closing of strands and wire is not taken into consideration.



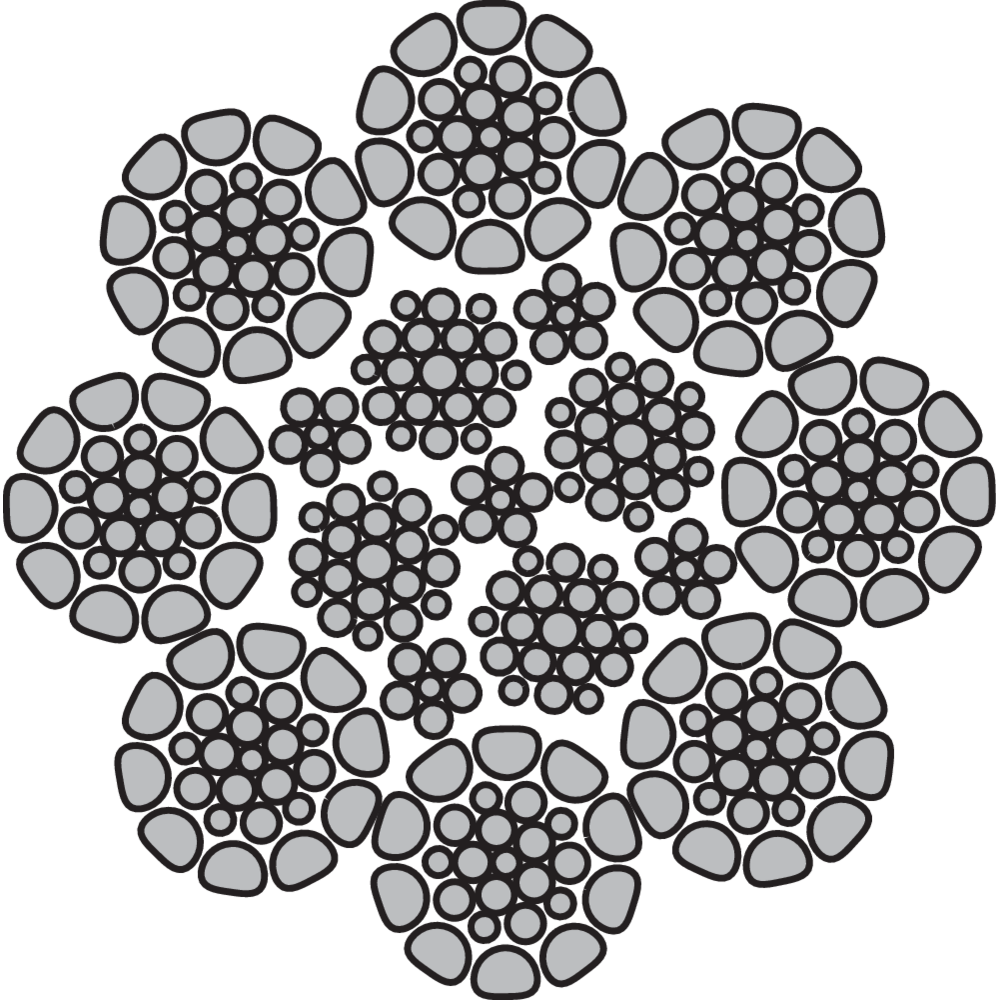
Special Wire Ropes
Demands for longer operation life and higher breaking loads have contributed to the development of "special wire ropes". These are to be used in demanding and tough environments when the ropes are used intensively.
The special wire ropes are often manufactured with high tensile wires and the strands are in many cases compacted to give a larger steel area and consequently a higher breaking load. This results in an increased working load for a specific rope diameter. Compacting of the rope also results in longer life and therefore a lower life cost.
Some areas of use demand wire ropes with better stability and extra low inner friction. For that purpose ropes are manufactured with a plastic coated steel core.
Special wire ropes can be double parallel which means that both wires and strands lay parallel to each other. This prevents wire cross over which can lead to wire indentations. Special wire ropes have a few things in common: less outer and inner friction, narrow tolerances, more flexible, more rounded and a larger contact surface against sheaves and drums. This results in a longer life in tough working conditions.














![Preform[new]_225mm_2](/sites/certex-fi/techdoc_import/Technical%20information%20general/STEEL%20WIRE%20ROPE%20PRODUCTS/OLD_Technical%20information/Steel%20wire%20rope/Technical%20description/10431/image-thumb__10431__product-large/preform-new-_225mm_2.ad488324.png)
![Strand lay length_eng[new]_225mm_2](/sites/certex-fi/techdoc_import/Technical%20information%20general/STEEL%20WIRE%20ROPE%20PRODUCTS/OLD_Technical%20information/Steel%20wire%20rope/Technical%20description/10432/image-thumb__10432__product-large/strand-lay-length_eng-new-_225mm_2.39628341.png)